

Modern digitizing oscilloscopes are very powerful analytical tools for use in signal analysis. However, to avoid misinterpretation of data, it is imperative that the operator of a digitizing oscilloscope be aware of the limitations and "quirks" of digitizing oscilloscopes. Despite the powerful capabilities of digitizing oscilloscopes, traditional analog oscilloscopes may be still be the better choice for certain measurements!
It is assumed that the reader has a basic understanding of how an analog oscilloscope works and also a basic understanding of the terminology associated with signal measurement. While analog oscilloscopes are often very "intuitive" to operate, digitizing oscilloscopes often require some period of time to become familiar with. The basic features of digitizing oscilloscopes are fairly easy to master, but becoming totally familiar with a particular unit often takes practice or daily use because of the bewildering array of signal acquisition and processing modes. To make matters worse, mastering the operation of a digitizing oscilloscope from manufacturer A does not mean that you can operate a unit from manufacturer B with the same proficiency!
Digitizing oscilloscopes make use of an analog-to-digital (A/D) converter early in the signal acquisition stage, whereas analog oscilloscopes perform all processing in the analog domain. Digitizing the input signal (the signal to be measured) early offers a multitude of processing and display options. However, because of the nature of digital signals, some limitations become inherent to the system, limitations which are not normally a problem if certain rules are adhered to. The details of the internal workings of digitizing oscilloscopes are not covered here; however, the reader can find such material on the web sites of major manufacturers of such equipment (HP, Tektronix, etc.).
Digitizing oscilloscopes offer some powerful advantages over conventional analog oscilloscopes. However, if the operator of the digitizing oscilloscope does not have an understanding of the concepts involved with such units, errors and/or misinterpretation of data may result.
Some of the primary reasons that digitizing oscilloscopes have limitations include:
Important: Because digitizing oscilloscopes have a finite (and rather shallow) memory depth, nearly all digitizing oscilloscopes have a sampling rate which is a function of time base setting. Failure to understand this relationship can lead to confusing or seemingly "bad" data for certain waveforms! This is one area where analog oscilloscopes prevail over digitizing oscilloscopes: the bandwidth (analogous to sampling rate in a digitizing scope) of an analog oscilloscope is constant regardless of the time base setting.
The reason that digitizing oscilloscopes reduce the sampling rate at long time base settings is not difficult to understand. Consider a digitizing oscilloscope that is labeled as a "100M s/s Digitizing Oscilloscope". Now suppose you wanted to observe a low frequency waveform with a period of 1 second. If the oscilloscope were to sample at 100M s/s for one second, it would require a memory 100 million samples deep! Not to mention that the display of the oscilloscope would not be able to display 100 million data points. Another way to look at it follows: Assume the digitizing oscilloscope has a memory of 10,000 samples (not at all uncommon). If we are to look at the same waveform (with a 1 second period), in order to make the memory "last" for 1 second the oscilloscope could sample the input data no faster than 10,000 s/s (a far cry from 100M s/s!). The fact that most digitizing oscilloscopes reduce the sampling rate as the time base increases is a critical factor to keep in mind when measuring signals. If you try to observe a signal with frequency components higher than half the sample rate, the oscilloscope will display erroneous data. This is because the sample rate is insufficient for the frequency content of the input waveform (the Nyquist sample rate theorem has been violated). In one sentence: When observing signals with a digitizing oscilloscope, you must ensure that the oscilloscope's sampling rate (at a given time base) is adequate for the frequency content of the input signal!
When using a digitizing oscilloscope to observe a waveform, you should have some idea of the nature of the waveform you plan to observe. Specifically, you should have some idea of the frequency characteristics of the waveform. If you are planning to look at a 1 MHz square clock waveform, you need an oscilloscope with a sample rate far higher than 1 MHz! Recall that square waveforms are actually made up of an infinite number of harmonically related sine waves. If you use a 1 MHz analog oscilloscope to observe a 1 MHz square wave, you will (at best) see only a sine wave because the harmonics of the waveform (which help to "square it off") are above the frequency range of the oscilloscope. As a general rule, I like to use an instrument that will reach to at least the 15th harmonic of a square waveform. For a 1 MHz 50% duty cycle clock, this means that a digitizing oscilloscope with a sample rate of at least 30 Ms/s (megasamples/second) is required! Fortunately, digitizing oscilloscopes are available that have sample rates in the Gs/s range.
Some waveforms are difficult to properly observe using digitizing oscilloscopes; these include waveforms such as amplitude modulated signals having a large carrier to modulating frequency ratio. For example, consider a waveform typical of an AM radio broadcast. For our example, we will assume that the waveform has a carrier frequency of 1MHz and the modulation signal is 1KHz. This represents a ratio (carrier frequency to modulating frequency) of 1000. Suppose we wish to observe one complete period of the modulating signal (which is 1KHz). For such a waveform to fit "nicely" on the CRT, the oscilloscope's time base would be set to .1msec/div. If we were to look at such a waveform on a conventional analog oscilloscope, the image on the screen would look similar to the figure below:
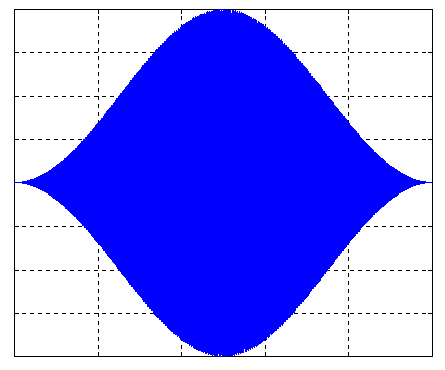
Even though we cannot see the individual cycles of the carrier (which is 1 MHz), the oscilloscope still traces them out on the display and the result is a "filled in" envelope. Now suppose we wish to observe this same signal using a typical digitizing oscilloscope. To have one period of such a waveform fit nicely on the oscilloscope display, we would once again set the time base to .1 msec/div (assuming the display is 10 div wide, which is typical). In order to capture the envelope of the signal "nicely", we will need at least 10 samples per cycle of carrier waveform. Since the carrier signal frequency is 1MHz, this means that the sampling frequency will need to be 10M s/s to provide a good display of the modulating signal envelope. Now comes the problem: with the "typical" digitizing oscilloscope, the memory of the unit will be filled far sooner than the amount of samples necessary to display one cycle of 1000 Hz! In reality, if the digitizing oscilloscope was set to a time base of say .1 msec/div, the oscilloscope would be sampling at a rate far below the rate necessary to properly capture a 1 MHz carrier signal. Using a digitizing oscilloscope on the same waveform as was measured with the analog oscilloscope would likely generate in image on the display similar to the one shown in Figure 2 below:
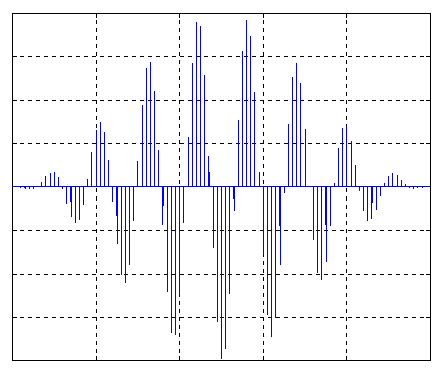
A casual glance at the image of Figure 2 indicates that it is very different from that of Figure 1. The image of Figure 2 is not representative of the true waveform characteristic. This example illustrates one pitfall that can occur to the "careless" operator of a digitizing oscilloscope!
While it is true that digitizing oscilloscopes offer tremendous capabilities, the operator must remember that the data that is acquired is only as good as the A/D converter in the unit (once things are "digital" it is rather easy to keep non ideal behavior to a minimum if proper design practices are adhered to). All A/D converters have quantizing noise and other non linear characteristics. Because digitizing oscilloscopes must often sample data at breakneck speeds (compared to the rates of digital audio for example) the A/D converters used are often of only 8 bits. So, just because an oscilloscope is "digital" does not mean that it is "perfect". Chances are however, that the results will be very good if the unit is operated within its limits!
On another topic, I am perplexed as to why digitizing oscilloscope manufacturers do not offer units with much larger memories. Memory prices have dropped tremendously in recent years. Good digitizing oscilloscopes can cost $10,000 to $20,000 or even far higher... when spending this much, why not up the price by $1000 and have tens or hundreds of megabytes of memory? The average home PC today has far more memory than the average $20,000 digitizing oscilloscope (HP and Tektronix take note!)
Part of the reason that digitizing oscilloscopes may not have large memories is because the resolution of data that can be displayed on a typical display may not exceed roughly 1000 "points" (assuming a typical 6" diagonal display). The manufacturer may think "Why capture more data that the screen can resolve?" A lousy decision in my opinion. Many applications could make great use of the "raw" data that digitizing oscilloscopes have to acquire anyway for them to work. Sure, the display cannot show 10 million data points, but the ability to export that amount of data on some type if magnetic media would be an extremely handy feature! The beauty of having access to the "raw" data is that the user can then process and display the data in any number of ways (using MATLAB, Excel, etc.).
End of page... come back soon... Aloha!